How Much Math Do You Need to Become a Data Scientist?
While data science is built on top of a lot of math, the amount of math required to become a practicing data scientist may be less than you think.
Have you ever considered a career in data science but been intimidated by the math requirements? While data science is built on top of a lot of math, the amount of math required to become a practicing data scientist may be less than you think.
The “Big Three” In Data Science
When you Google the math requirements for data science, the three disciplines that consistently come up are calculus, linear algebra, and statistics. The good news is that — for most data science positions at least — the only kind of math you need to become intimately familiar with is statistics.
Calculus
For many people with unpleasant memories of mathematics from high school or college, the thought that they’ll have to re-learn calculus is a real obstacle to becoming a data scientist.
In practice, while many elements of data science depend on calculus, you may not need to (re)learn as much as you might expect. For most data scientists, it’s really only vital to understand the principles of calculus and how those principles might affect your models.
If you understand that the derivative of a function returns its rate of change, for example, then it’ll make sense that the rate of change trends toward zero as the graph of the function flattens out.
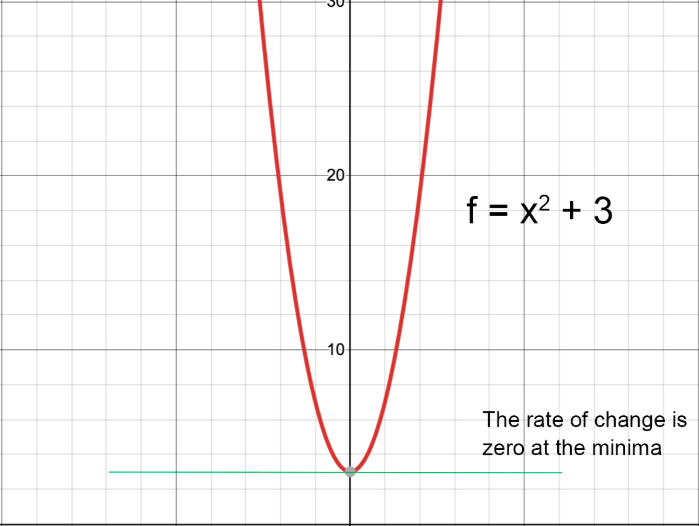
That, in turn, will allow you to understand how gradient descent works by finding the local minima for a function. It’ll also make it clear that a traditional gradient descent only works well for functions with a single minima. If you have multiple minima (or saddle points), a gradient descent might find a local minima without finding the global minima unless you start from multiple points.
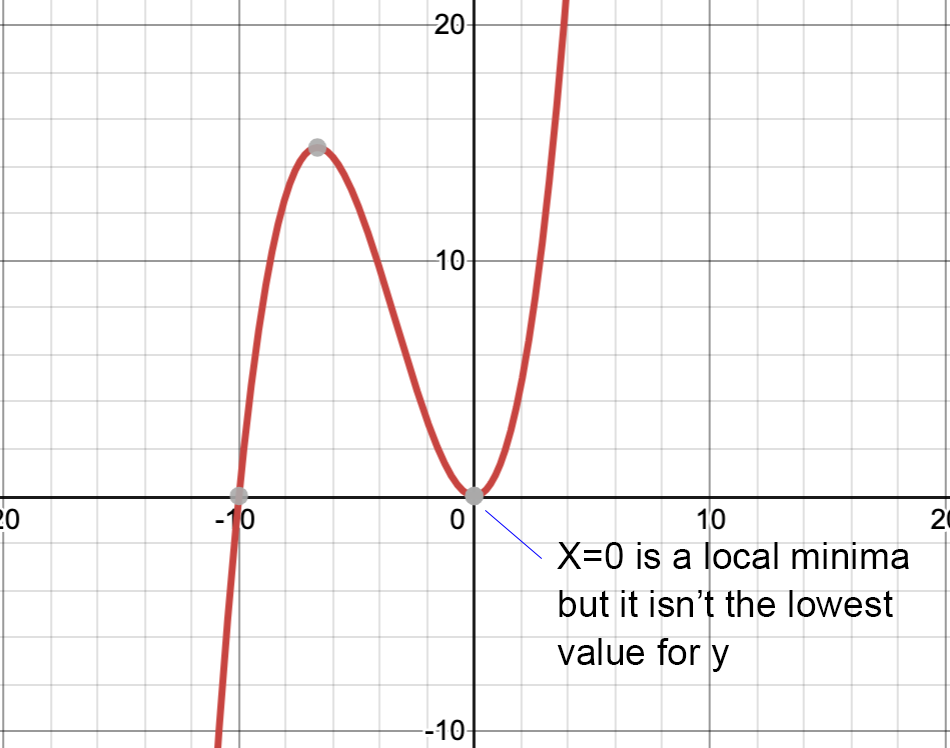
Now, if it’s been a while since you did high school math, the last few sentences might sound a little dense. But the good news is that you can learn all of these principles fairly quickly. And it’s way less complicated than being able to algebraically solve a differential equation, which (as a practicing data scientist) you’ll probably never have to do — that’s what we have computers and numerical approximations for!
Want to try your hand at Data Science? Try out our Free Data Science Prep Work and test-run the material we teach in the course.
Linear algebra
In data science, your computer is going to be using linear algebra to efficiently perform many required calculations. If you perform a Principal Component Analysis to reduce the dimensionality of your data, you’ll be using linear algebra. If you’re working with neural networks, the representation and processing of the network are also going to be performed using linear algebra. In fact, it’s hard to think of many models that aren’t implemented using linear algebra under the hood for the calculations.
At the same time, it’s very unlikely that you’re going to be handwriting code to apply transformations to matrices when applying existing models to your particular data set. So, again, understanding the principles will be important, but you won’t need to be a linear algebra guru to model most problems effectively.
Probability and statistics
The bad news is that this is a domain you’re really going to have to learn. And, if you don’t have a strong background in probability and statistics, learning enough to become a practicing data scientist will take a significant chunk of time. The good news is that there is no single concept in this field that’s super difficult — you just need to take the time to really internalize the basics and then build from there.
Even more math
There are lots of other types of math that may also help you when thinking about how to solve a data science problem. They include:
Discrete math
This isn’t math that won’t blab. Rather, it’s mathematics dealing with numbers with finite precision. In continuous math, you are often working with functions that could (at least theoretically) be calculated for any possible set of values and with any necessary degree of precision.
As soon as you start to use computers for math, you’re in the world of discrete mathematics because each number only has so many “bits” available to represent it. There are several principles from discrete math that will both serve as constraints and inspiration for approaches to solving problems.
Graph theory
Certain classes of problems can be solved using graph theory. Whether you’re looking to optimize routes for a shipping system or building a fraud detection system, a graph-based approach will sometimes outperform other solutions.
Information theory
You’re going to bump up along the edges of information theory pretty often while learning data science. Whether you’re optimizing the information gained when building a decision tree or maximizing the information retained using Principal Component Analysis, information theory is at the heart of many optimizations used for data science models.
The good news
If you’re terrified of math or unwilling to ever look at an equation, you’re not going to have much fun as a data scientist or data analyst. If, however, you have taken high school-level math and are willing to invest some time to improve your familiarity with probability and statistics and to learn the principles underlying calculus and linear algebra, then math should not get in the way of you becoming a professional data scientist.
Ready To Get Started In Data Science?
As a next step, we’d encourage you to Try out our Free Data Science Prep Work to see if data science is right for you.
If you realize you like it, apply today to get started learning the skills you need to become a professional Data Scientist.
Not sure if you can do it? Read stories about students just like you who successfully changed careers on the Flatiron School blog.
Disclaimer: The information in this blog is current as of 9 November 2023. Current policies, offerings, procedures, and programs may differ.



