Artificial neural networks are a class of machine learning algorithms. Their creation by Warren McCullough and Walter Pitts in 1944 was inspired by the human brain and the way that biological neurons signal one another. Neural networks are a machine learning algorithm since the algorithm will analyze data with known labels so it can be trained to recognize images that it has not seen before.. For example, in the Data Science Bootcamp at Flatiron School one learns how to use these networks to determine whether an image shows cancer cells present in a fine needle aspirate (FNA) of a breast mass.
Neural networks are comprised of node (artificial neuron) layers, containing the following:
- an input layer
- one or more hidden layers
- an output layer
A visual representation of this is on view in the figure below. (All images in the post are from the Flatiron School curriculum unless otherwise noted.)
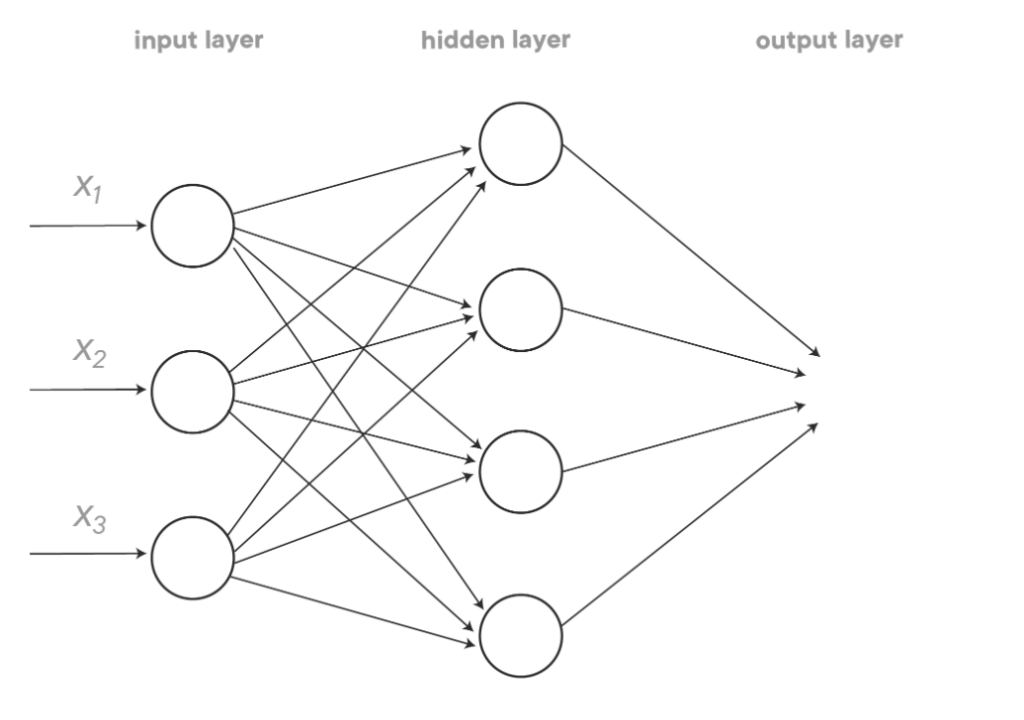
Each node connected to another has an associated weight and threshold. If the output is above the specified threshold value, then the node activates.. This activation results in data (the sum of the weighted inputs) traveling from the node to the next layer that is composed of nodes. However, if the node is not activated, then it does not pass data along to the next layer. A popular subset of neural networks are deep learning models, which are neural networks that have a large number of hidden layers.
Neural Network Activation Functions
In this post, I would like to focus on the idea of activation, and in particular the hyperbolic tangent as an activation function. Simply put, the activation function decides whether a node should be activated or not.
In mathematics, it is common practice to start with the simplest model. In this case, the most basic activation functions are linear functions such as y=3x-7 or y=-9x+2. (Yes, this is the y=mx+b that you still likely recall from algebra 1.)
However, if activation functions are linear for each layer, then all of the layers would be equivalent to a single layer by what are called linear transformations. It will take us too far afield to discuss linear transformations, but the upshot is that nonlinear activation functions are needed so that the neural network can meaningfully have multiple layers. The most basic nonlinear functions that we can think of would be a parabola (y=x^2), which can be seen in the diagram modeling some real data.
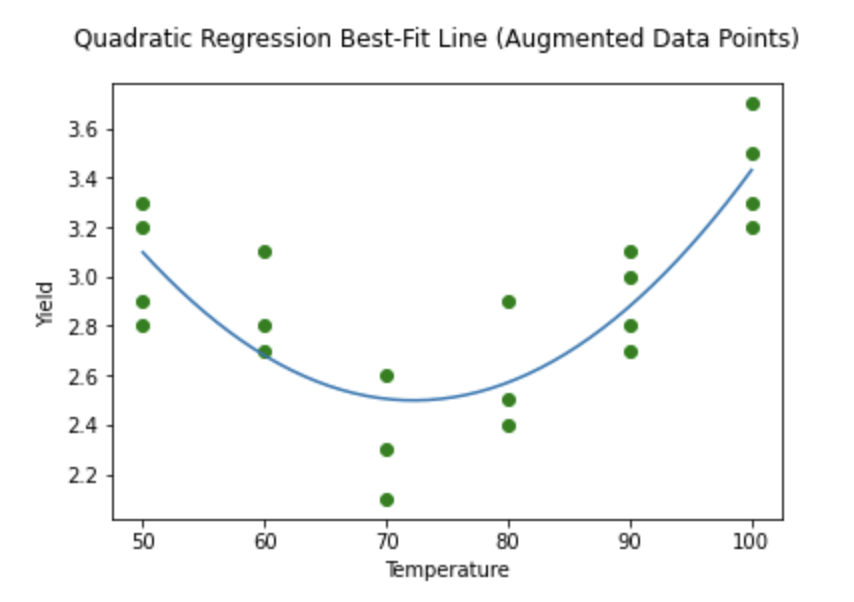
While there are a number of popular activation functions (e.g., Sigmoid/Logistic, ReLU, Leaky ReLU) that all Flatiron Data Science students learn, I’m going to discuss the hyperbolic tangent function for a couple of reasons.
First, it is a default activation function for Keras, which is the industry standard deep learning API written in Python that runs on top of TensorFlow, which is taught in detail within the Flatiron School Data Science Bootcamp.
Second, the hyperbolic function is an important function even outside of machine learning and worth learning more about. It should be noted that the hyperbolic tangent is typically denoted as tanh, which to the mathematician looks incomplete since it lacks an argument such as tanh(x). That being said, tanh is the standard way to refer to this activation function, so I’ll refer to it as such.
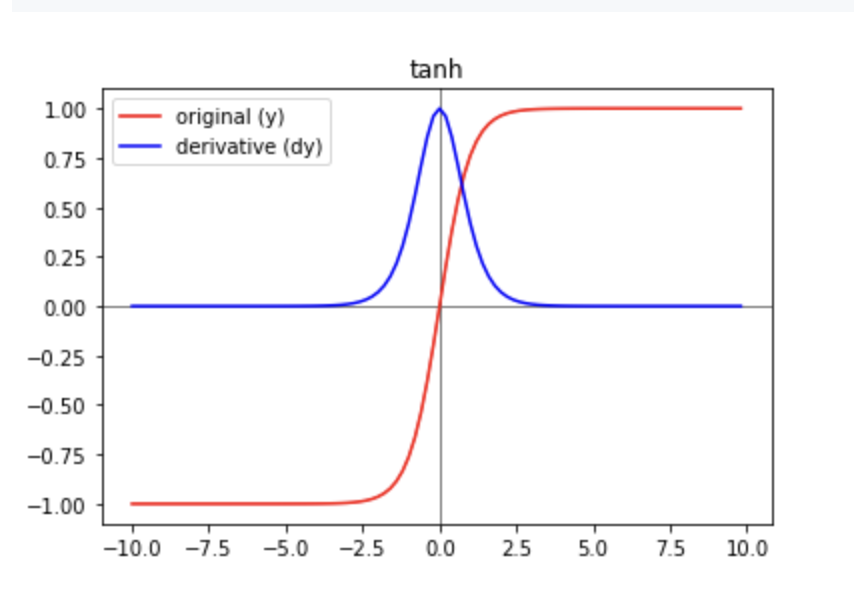
Neural Network Hyperbolic Functions
The notation of hyperbolic tangent is pointing at an analog to trigonometric functions. We hopefully recall from trigonometry that tan(x)=sin(x)/cos(x). Similarly, tanh(x)=sinh(x)/cosh(x), where sinh(x) = (e^x-e^-x)/2 and cosh(x) = (e^x+e^-x)/2.
So we can see that hyperbolic sine and hyperbolic cosine are defined in terms of exponential functions. These functions have many properties that are analogous to trigonometric functions, which is why they have the notation that they do. For example, the derivative of tangent is secant squared and the derivative of hyperbolic tangent is hyperbolic secant squared.
The most famous example of a hyperbolic function is the Gateway Arch in St. Louis, MO. The arch, technically a catenary, was created with an equation that contains the hyperbolic cosine.

(Note: This image is in the public domain)
High voltage transmission lines are also catenaries. The formula for the description of ocean waves not only uses a hyperbolic function, but like our activation function uses than.
Hyperbolic Activation Functions
Hyperbolic tangent is a sigmoidal (s-shaped) function like the aforementioned logistic sigmoid function. Where the logistic sigmoid function has outputs between 0 and 1, the hyperbolic tangent has output values between -1 and 1.
This leads to the following advantages over the logistic sigmoid function. The range of [-1, 1] tends to make:
- negative inputs mapped to strongly negative, zero inputs mapped to near zero, and positive inputs mapped to strongly positive on the tanh graph
- each layer’s output more or less centered around 0 at the beginning of training, which often helps speed up convergence
The hyperbolic tangent is a popular activation function that is often used for binary classification and in conjunction with other activation functions that have many nice mathematical properties.
Interested in Learning More About Data Science?
Discover information about possible career paths (plus average salaries), student success stories, and upcoming course start dates by visiting Flatiron’s Data Science Bootcamp page. From this page, you can also download the syllabus and gain access to course prep work to get a better understanding of what you can learn in the program, which offers full-time, part-time, and fully online enrollment opportunities.




